Числа Фибоначчи это что такое: последовательность чисел + финансы, расчеты, история
Что такое числа Фибоначчи? Человек далекий от мира математики, может и не ответить на этот вопрос. А меж тем, последовательность фибоначчи используется не только в программировании и трейдинге, но и во многих других сферах. Сегодня мы поговорим о том, как числа этой последовательности нашли применение в математике. Разберемся с тем, что это вообще такое и поговорим о других числовых последовательностях и аномалиях. И, конечно, разберемся с тем, откуда вообще взялось такое название.

О чем вообще речь?
Итак, числа Фибоначчи являют собой соответствующую последовательность от 0 и до бесконечности. Они урегулированы несколькими правилами:
- В каждом элементе последовательности первые 2 числа будут равны нулю и единице.
- Последующее число должно быть равным сумме 2-х предыдущих чисел.
Названа эта последовательность была в честь Фибоначчи. Для тех кто не знает: Фибоначчи это математик Леонардо Пизанский. Он жил во времена Средних веков.
Откуда вообще взялась эта последовательность?
А вот тут не все так просто. Все дело в том, что эта последовательность была известна еще до того, как ее назвали в честь Фибоначчи. Об этих числах знали во времена существования древней Индии. На тех территориях заявленную последовательность применяли в некоторых метрических науках. Одной из таких наук стала просодия. Это сложение стихов, если расшифровывать. И в Индии о последовательности Фибоначчи узнали намного раньше, чем ее так стали называть.
Просодицисты (те, кто занимался просодией), сумели доказать, что число элементов в n-длину, будет суммировано двумя предыдущими числами в последовательности. Ну а Леонардо Пизанский занялся исследованием этой необычной последовательности на Западе. Это раскрывается в его труде под названием "Книга абака".
О книге Абака
В оригинале эта книга называется Liber abaci. Это название книги на латыни. Считается главным трудом Леонарда Пизанского (Фибоначчи). Как раз этот труд считается главной работой жизни Леонардо Пизанского. У книги было несколько версий:
- 1202 год.
- 1228 год.
К сожалению, до наших дней дошла только одна (переработанная) версия, она была посвящена М. Скоту.
Кто такой Майкл Скот: это ученый живший на территории Шотландии, который занимался философией, математикой и переводами. Именно благодаря тому, что Майкл Скот занимался переводами на латыни, ученые из стран Европы сумели получить доступ к различным трудам арабских и античных мыслителей. Майкл Скот был известен и Фибоначчи. Но о нем поговорим чуть позже.
Л. Пизанский называл абаком различные арифметические вычисления. А сам труд был посвящен изложению десятичной арифметики. О десятичной системе счисления поговорим немного позже.
Леонардо Пизанский был знаком с достижениями индийцев и древних греков. Он изучал арабские переводы трудов. И он же занялся систематизацией этих работ, собрав все в одном научном труде. Он систематизировал большую часть работ из древней Греции и Индии, в своей книжке. Тут важно понимать еще и то, что разобраться в трактатах рядовой человек попросту не мог. Даже со знаниями языков и письменности. Все дело в том, что книга, написанная Фибоначчи, имела более понятное для обывателя повествование. Простой язык и позволил Фибоначчи донести до рядового читателя основы практического счета. Если вообще можно говорить о "рядовом читателе" в те времена. Все-таки стоит понимать, что доступные для всех книги появятся намного позже.
Изложение Фибоначчи было по глубине, полноте и ясности на порядок лучше, чем то, что было в исламских и античных источниках. Можно с уверенностью сказать, что книга абака это одни из лучших трудов в те времена. И до эпохи Декарта, книге абака даже альтернатив не было.
В этом труде есть 15 книг (проще называть их главами).
В первой книге абака содержатся арабо-индийские цифры. Тут же описан алгоритм умножения. Надо сказать, что алгоритм умножения по Фибоначчи, гораздо проще того, что было в римской системе. Плюс к тому, здесь описан механизм преобразования чисел в новую систему, из старой. А еще именно Фибоначчи введет понятие нуля, как самостоятельного числа. Во второй книге есть практика по денежным расчетам. Именно благодаря этой части труда, книга абака стала столь популярной и ценной для всех, кто занят счетом в той или иной степени.
В третьей книге есть изложение разнообразных математических задач. Там же содержатся некоторые теоремы, описания прогрессий и т.п.
В следующей книге содержится методология приближенного вычисления. Там же есть способы геометрического построения иррациональных чисел и корней. Ну а после этого Фибоначчи использует различные дополнения и способы решения уравнений. Есть теория делимости, есть задача о кроликах. Кстати, именно эта задача приводит к известной последовательности Фибоначчи.
И о многих важнейших задачах все узнали как раз в книгах Фибоначчи. Даже при изложении стандартных, и в каком-то роде классических задач, он позволил посмотреть на них по-новому. Более того, методология решения математических задач в основном оригинальная. Да, символика отсутствует, но суть не меняется. Плюс к тому, именно Леонардо пошел в этой области гораздо дальше, чем китайцы. И именно Фибоначчи стал первым человеком на территории Европы, который стал свободно работать с отрицательными числами. Он трактовал их как долги, это индийская интерпретация. Фибоначчи успел открыть несколько численных методов. Правда некоторые из этих методов уже были известны арабам до этого.
Стоит сказать, что книга абака стала трудом, оказавшим очень серьезное влияние на распространение знаний о математике на территории Европы. Книга абака стала неоценимым трудом. Именно с ее помощью по Европе распространялись индийские цифры и десятичная система счисления. Плюс к тому, она стала своеобразным учебником для ученых Европы.

О задаче про кроликов
Последовательность была изучена Фибоначчи на примере задачи с кроликами. Он решил смоделировать эту последовательность на примере биологически противоречивой (фантастической) схеме размножения популяции кроликов. Естественно, такая схема размножения кроликов не может повториться в реальности, но кроликов считать проще, чем множества и числа.
Итак, у нас есть изначальные условия:
- Есть 1 кролик.
- Есть 1 крольчиха,
- Есть 2 новорожденных кролика.
Уже со 2-го месяца кролики начинают спариваться. И каждый раз кролики производят по паре новых кроликов, практически каждый месяц. Тут есть 2 особенности: кролики в реальности не размножаются уже через 2 месяца. Но таковы условия задачи. Плюс к тому, мы имеем дело с бессмертными кроликами.
Все что нам предлагает тут найти: количество пар из кроликов через условные 12 месяцев.
Алгоритм размножения кроликов с такими входными условиями будет достаточно понятным. В самом начале месяца №1 у нас есть 2 кролика (пара новорожденных). Уже к концу месяца №1 у нас есть пара кроликов после спаривания. К концу месяца №2 у нас есть новорожденная пара. Теперь кроликов становится 4. Первая пара кроликов опять спаривается. Уже в конце месяца №3 пара под номером 1 родит еще двух крольчат, и снова произойдет спаривание. Во второй паре начнет спаривание. К четвертому месяцу родится очередная пара кроликов, и случится очередной спаривание. Еще рождается новое потомство от второй пары. Ну а третья пара кроликов начинает спариваться.
Достаточно сложная и структурная схема, но по итогу у нас получается, стандартная последовательность Фибоначчи. Достаточно взглянуть на формулу, чтобы это понять. Кстати, есть предположение, связанное с тем, что именно эта задача могла стать первой задачей, связанной с моделированием экспоненциального роста популяции.
Интересно и то, что последовательность Фибоначчи начали так называть только в 19-м веке. Этот термин начал использовать Эдуард Люка, теоретик.
Как используются числовые последовательности?
Начнем с того, что некоторые сомневаются в том, что числа Фибоначчи вообще имеют какой-то смысл в природных и исторических явлениях. По мнению скептиков, это подгонка под нужный результат, а не совпадение. Но дело все в том, что как раз числа Фибоначчи находят свое отражение в разных сферах. И не только в природе.
В кодировании используются коды Фибоначчи. Основанием этих кодов являются иррациональные числа. Числа Фибоначчи можно обнаружить и в музыке, и в поэзии. В какой-то степени, в поэзии их и начали применять изначально.
Кроме того, есть такое понятие как золотое сечение. Это "отношение", связанное через формулу Бине напрямую с последовательностью Фибоначчи.
Но и на этом все не заканчивается. Ведь последовательность Фибоначчи встречается даже у растений:
- Ананасы.
- Лепестки цветов.
- Сосновые шишки.
- Семена подсолнуха и т.п
Все вышеперечисленное удивительным образом растет так, что можно обнаружить последовательность Фибоначчи.
Есть последовательность и в филлотаксисе. Для тех кто не знает, это схема расположения листов у растений. Так вот, если у листьев есть спиральное листорасположение на приросте 1 года, то здесь тоже используется последовательность Фибоначчи. Это не шутка, вы можете почитать об этом подробнее в открытых источниках.
Что такое золотое сечение (кратко)
Ну и раз мы затронули формулу Бине и числа Фибоначчи, без золотого сечения тоже не обойтись. Наверняка о нем слышал каждый. Но что это значит? Золотое сечение это единственное в своем роде отношение:
- Целого.
- Частей.
Отношение частей складывается таким образом, что части в нем равны между собой. Более того, части равны к целому. Каждая часть равна к целому. Именно на "золотых отрезках" и базируются некоторые методики "пропорционирования" в архитектурных проектах. Это отношение есть и в науке, искусстве и природе.
По сути, соотношение это является универсальным. И в эпоху Возрождения это название и появилось. Все началось с труда Луки Пачоли. Он в своем трактате описал божественную пропорцию. Интересно и то, что европейцы и тут не стали первопроходцами. Потому что закономерность отношений подобного характера, была отмечена и ранее. Например, во все той же злополучной Греции (эпоха античности), в Египте и Месопотамии.
Например, в математике древней Греции золоте сечение было делением отрезка от а до б, по точке с. Тут важно было разделить отрезок так, чтобы большая часть относилась к меньшей точно так же как и весь отрезок относился к большей части. Фактически, это понятие разделяли на произвольные величины.
В силу того, что в математическом доказательстве используется много чисел, здесь есть и "золотое число" Это Фи. Кстати, значение фи имеет собственное установленное значение в 1.62. Это не такая постоянная, как число П. И вместе с тем, используется приблизительное значение.
Если сводить все к процентному соотношению (с округлением), то величина будет разделена на 2 части:
- 38 процентов.
- 62 процента.
Интересно и то, что у золотого сечения полно превосходных свойств. Но не нужно забывать о том, что приписывают ему едва ли меньше свойств. Скорее всего даже куда больше, чем золотое сечение имеет.
История открытия золотого сечения нам доподлинно неизвестна. Но мы знаемо том, что уже в труде "Начала", который был написан Евклидом, оно уже использовалось. Это 300 лет до нашей эры (примерная датировка). Там способ деления отрезка применяется для того, чтобы построить правильный 5-угольник. И вот именно с того момента, когда Лука Пачоли добрался до золотого сечения, оно начало обретать какую-то совсем уж "божественную сущность". Ничего удивительного в этом естественно нет. В давние времена, даже химии, как самостоятельной науки не было. Зато была алхимия.
Кстати, Пачоли был другом и современником Леонардо да Винчи. По мнению этого францисканца эта пропорция отражала настоящее триединство Бога.
Не совсем понятно, откуда взяли термин золотого сечения. Некоторые авторитетные источники связывали авторство термина с Леонардо да Винчи. Следовательно, это 15й век. Другие относят появление термина уже к 16 веку.
Все что мы знаем, это то, что первое упоминание термина было зафиксировано в 1835 году. Оно находится в материалах Мартина Ома. Это издание "Чистой элементарной математики", а сам термин расположен в одном из примечаний. Ом писал, что это сечение довольно часто называют золотым. Интересно и то, что Ом по всей видимости не стал придумывать этот термин сам. Хотя есть и противники этой версии, настаивающие на авторстве Мартина Ома.
Интересно и то, что в первом издании своей книги по математике, Ом не стал использовать этот термин. По мнению некоторых исследователей, термин мог появиться в первой четверти 19 века. По мнению другого исследователя (М. Ливио), термин стал очень популярен в немецкой устной традиции. По крайней мере мы можем точно утверждать, что Ом стал виновником распространения термина золотого сечения в немецкой литературе, посвященной математике.
О сфере применения золотого сечения
Применение золотого сечения может быть как сознательным, так и случайным. Впрочем, в случае с природой, случайность золотого сечения тоже подвергается сомнениям. Разбираться в случайности или намеренности золотого сечения не будем, оставим этот вопрос философам. А пока поговорим о том, где оно встречается.
Достоверно точно известно, что в искусстве, уже после Леонардо да Винчи, некоторые мастера начали осознанно использовать пропорции золотого сечения в своих проектах. Причем это касается не только живописи. Оно нашло свое применение даже в произведениях Баха. Кроме того, используют золотое сечение и по сей день. Например, у Пенроуза есть мозаика, наглядно демонстрирующая способ применения золотого сечения.
В искусстве золотое сечение применялось меж тем, и до Леонардо да Винчи. Например, в доказательство некоторых утверждений гипотезы, легли некоторые очень древние правила. Фактически, эти знания были получены от древних египтян, пусть и не напрямую, а через искусство. Все дело в том, что золотые пропорции есть в пирамиде Хеопса. Они встречаются даже в гробнице Тутанхамона. По всей видимости, при изготовлении украшений и барельефов, а также отдельных помещений храмов, египтяне пользовались как раз принципом золотого сечения. Кстати, этим все не ограничивается.
Все дело в том, что фасад Парфенона тоже не был лишен этого универсального сечения. Даже в документации из г. Помпеи, были заложены соответствующие пропорции. Интересно и то, что золотое сечение не является понятным для обывателя. Например, в фотосъемке, используемые пропорции, не кажутся идеальными. По сути, большинство людей не может воспринимать "золотое сечение", как нечто идеальное и потрясающее.
Что касается природы, то тут не все так просто. В какой-то степени, золотое сечение является скорее матричным эталоном. А поскольку эволюция подразумевает приспособление, и отход от канонов, не всегда оно встречается в природе.
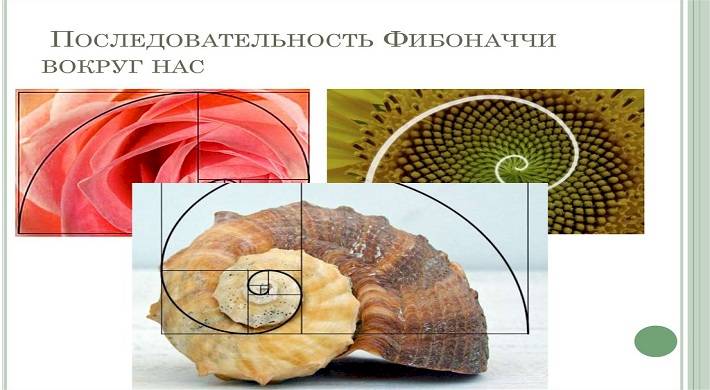
О природных примерах золотого сечения
А вот теперь пора поговорить о том, как золотое сечение обнаруживается в науке. Например, оно очень тесно увязано на симметрию 5 порядка. А именно, трехмерные представители этого сечения в симметрии это:
- Икосаэдр.
- Додекаэдр.
Можно с уверенностью заявить о том, что, где появятся производные или структурные фигуры, будет найдено золотое сечение. В какой-то степени это уже аксиоматичное утверждение, но можно ознакомиться и с доказательствами. Кроме того, у некоторых молекул воды при определённых условиях можно обнаружить вышеперечисленные фигуры.
Кроме того, золотое число обнаруживается в различных физических задачах. Не только в электрических цепях, но в геофизике. Вообще примеры научных направлений, в которых применяется золотое сечение, можно перечислять в буквальном смысле до бесконечности.
Об архитектурном применении
Принцип золотого сечения очень часто применяется как раз в архитектуре. Интересно и то, что один из торговых домов, архитектура которого сочетает в себе золотые пропорции, был построен в России. Он располагается на пересечении двух улиц:
- Мойка.
- Гороховая.
Золотое сечение отражается начиная с длины этого здания. Кроме того знаменитый Исаакиевский собор внезапно тоже попал в золотой треугольник. Интересно и то, что гармоничная конструкция у профессиональных архитекторов, мастеров искусства и других талантливых людей, хранится чуть ли не на подкорке. Некоторые конечно стараются осознанно применять золотое сечение. Но у некоторых оно может быть и на уровне подсознания.
Еще одним популярным примером является здание МГУ (Воробьевы горы).
Обнаружить золотой треугольник невооруженным взглядом будет трудно, поэтому предлагаем вам изучить зону центральной башни. Там при подробном рассмотрении, обнаруживается та самая золотая пропорция.
И, конечно, золотое сечение обнаруживать начали впервые в архитектуре Древнего Египта. Например, пропорции, в которых построена пирамида Хеопса, как раз соответствуют золотому числу. Все дело вот в чем:
- У нас треугольник с углом (прямым).
- 1 катет этого треугольника является высотой.
- Второй катет этого треугольника является 0.5 основания.
Если прямо сегодня взять отношение гипотенузы к одной из сторон (меньшей), то получится практически идеальную "фи". Кстати, если в природе золотое сечение оказалось еще хоть как-то объяснимым, то с архитектурой не все так просто. В какой-то степени, золотое сечение в архитектуре стало своеобразной неожиданностью. И ведь довольно странная ситуация: тот же Парфенон в Древней Греции строили с уникальными пропорциями, которые соответствуют золотому сечению.
И вот откуда взялось золотое сечение в пропорциях и архитектуре, не совсем понятно. Потому что первые его упоминания, как какого-то "невероятного совпадения", были сильно позже тех датировок, в которые строились здания. Ведь у очень многих зажиточных людей дома строились как раз с сознательным использованием этого золотого сечения.
Как используются числа Фибоначчи python?
Мы уже разобрались с тем, как применяется золотое сечение Леонардо да Винчи. Теперь вернемся к вопросу последовательности Фибоначчи. И тут стоит сказать, что профессиональные программисты порядком подустали от этих чисел. Потому что примеров их вычисления достаточно много.
Например, для вычисления малых n, используется небольшой скрипт с простой сортировкой. Минус этого решения в том, что нужно использовать операции с плавающими запятыми. А это не самая удобная система вычисления. Хотя бы потому, что для больших чисел n приходится использовать повышенную точность вычисления.
И еще одна проблема: комплексные числа. Тут все сводится к эстетике. С одной стороны, применение комплексных чисел для счета F(n) с математической точки зрения, более приемлемый вариант. С другой же стороны, код для вычисления вызывает нервный тик у любого специалиста уровня middle.
Самым простым решением является рекурсия. Кстати, рекурсия записывается в одну строчку. Это один из простых вариантов работы с числами Фибоначчи. Но и тут не все так просто. Да, повторить определение из математики тут в разы проще. Но время выполнения растёт по экспоненте. Особенно если мы говорим о том, что нужно считать большое значение n. Исполнение будет очень долгим, и с этим придётся смириться, потому что альтернативных решений для рекурсии нет. Ну и конечно, есть еще одна дополнительная проблема: стек переполняется.
Есть и альтернативный вариант. Это операция запоминания. Рекурсия предполагает вычисления, которые пересекаются. Пересечений столько, что некоторые значения приходится считать по 2-3 раза. Поэтому тут нужно использовать механизм запоминания, который будет исключать уже посчитанные числа. В этом случае можно использовать декоратор, простой массив или словарь.
У этого преимущества есть как недостатки, так и преимущества. Преимущество в том, что рекурсия может быть превращена в готовое решение с возможностью запоминания. Время исполнения кода перестает быть экспоненциальным, и становится линейным. И в этом случае будет потрачено больше памяти. В этом же и раскрывается недостаток такого решения.
И от переполнения стека программист не застрахован и здесь. Но именно это самый простой и оптимальный для решения вариант.
Далее мы можем рассмотреть решение с динамическим программированием.
Рекурсивные вызовы в этом случае будут отсутствовать как явление. С другой стороны, здесь есть недостаток связанный с временем выполнения, оно всё еще остается линейным. И для малых n это еще работает. И код довольно простой. Но с большими n это становится своеобразной проблемой.
Реже всего пытаются использовать матричную алгебру. По мнению специалистов, это как раз идеальный вариант. Как с точки зрения расходов памяти и времени. Так и с математической позиции. Правда тут нужно уметь использовать матрицы. Правда код здесь получится достаточно объемным. С другой стороны, время становится логарифмическим. Объем памяти фиксируется. Ну и конечно, без понимания матриц, делать здесь нечего.
А еще существует фибоначчиева система счисления.
О системе счисления
Это система счисления (смешанного типа), для применения целых чисел, на базе последовательности Фибоначчи. Используется преимущественно там, где используются информационные технологии. В какой-то степени, именно информационные технологии и стали естественной сферой использования. Впрочем, одной информационной сферой и IT все не ограничивается.
В фундаменте этой системы счисления используется теорема Цекендорфа.
Используется Фибоначчиева система счисления в арифметике. В арифметике для сложения некоторых чисел, в системах счисления позиционного вида есть проблема переполнения разряда. Там используется стандартный перенос, который позволяет исключить проблему наполненности разряда.
Но с системой счисления по Фибоначчи, все не так просто.
В информатике последовательность Фибоначчи в целом, и система счисления в частности, применяется для выстраивания кодировки стандартных (натуральных) чисел. Как раз эта система счисления подойдет для тех чисел, что используют последовательные строчки битов. Но в этой системе счисления исключена комбинация из двух единиц. Используется она лишь как финальный маркер окончания записи.
Кстати, для работы с кодом Фибоначчи нужно переписывать все цифры в обратном порядке. Но не все так просто как может показаться.
Еще одним практическим применением системы счисления построенной на числах Фибоначчи, является абака, использовавшаяся у инков. Для тех кто не знает ,что такое абака, нужно дать отдельное разъяснение.
Абаком называют целую серию счетных арифметических досок. С их помощью производили простые арифметические вычисления не только на территориях Китая, но в Риме, а также Греции. Сегодня естественно они не используются. Но вот что интересно, есть несколько разновидностей абаков, которые могли применяться с системой счисления по Фибоначчи. Правда тут у нас всего лишь предположение, а не железное утверждение. Использоваться эта система счисления могла для упрощения подсчета зерна.
Ну а теперь о том, как используют последовательность Фибоначчи в трейдинге.
О криптотрейдинге
Фибоначчи активно используется в трейдинге, и в особенности, в инструментах для технического анализа. Как вы можете знать, цена на любой актив не может постоянно сохранять свой тренд. Цены меняются, на рынке происходят различные события, которые конечно тоже не стоит выбрасывать из головы. Тренд поменяется и корректируется. А может и просто повернуться в диаметрально противоположном направлении.
Трейдер фиксирует импульсы, которые предсказывают рост цены или ее снижение. Так или иначе, но после определенного момента, цена начинает корректироваться. Это называется коррекционным движением. Предсказать глубину, на которую цена откатится, достаточно проблематично. Но все-таки возможно. Для этого используется разнообразный инструментарий для технического анализа. Как раз при помощи отдельных индикаторов и инструментов, можно предсказывать объем коррекции.
Посредством уровней Фибоначчи можно реализовать коэффициенты. Именно с их помощью можно получать актуальные данные о том, как работает рынок сегодня, и какие прогнозы могут появиться уже в ближайшее время
Инструмент Уровни Фибоначчи позволяет фиксировать внутритрендовую коррекцию. Традиционно, для этого инструмента используются уровни:
- 38.2
- 61.8.
- 50.0
- 61.8 и т.п.
Нужно заметить, что именно от уровней зависит действие трейдера. Кроме того, уровень в 50, например, не имеет к числам Фибоначчи никакого отношения. Все дело в том, что глубина корректировки цены чаще всего равна половине первоначального импульса. Уровни, которые используются в трейдинге, обычно формируют так называемую сетку "Фибо". Они нужны для определения того, какой глубины коррекция достигла. Разумеется речь о трендах:
- Бычьих.
- Медвежьих.
Ну и конечно, посредством этой сетки можно определять уровни сопротивления и поддержки. Кроме того, уровни фибоначчи обычно ложатся в базис какого-то конкретного индикатора. Есть и одноименный инструментарий, который можно развернуть в рамках популярных трейдинговых терминалов.
Можно использовать уровни для сочетания с другими индикаторами. Например, сочетать с MACD. А можно применять фибоначчи в связке с фигурами тех. анализа. Но тут не все так просто, и без въедливого изучения вопроса точно не удастся разобраться. Исходная точка для работы с уровнями, это всегда минимальная цена, в момент восхождения тренда. Ну и максимальное значение используют при условии, что цена начала падать, а значит тренд стал нисходящим.
Помимо уровней, существует еще и так называемый веер. Это не фигура технического анализа, но полноценный инструмент для торговли. Этот веер может быть использован для выявления потенциальных уровней сопротивления и поддержки. Кроме того, веер может пригодиться и для детектирования зоны разворота тренда. Важно: речь о возможной зоне разворота тренда, а не уже о фактической.
Стратегия торговли с веером будет практически идентичной. Иными словами, долго с уровней переучиваться не придется, общий смысл торговли с использованием веера сохраняется. Разница только в том, что уровни отображаются по горизонтали. А вот в случае с веером, все полоски будут под определенным углом. И чем дальше по графику, тем сильнее отклонение уровня.
Ну и конечно не стоит забывать о таком инструменте, как расширение. Вот только расширение позволяет анализировать потенциал изменения ценового импульса. Сюда добавляются и дополнительные возможности. Посредством расширения можно будет оценивать масштаб надвигающегося изменения, путем оценки потенциального импульса цены.
Но тут важно помнить о том, что расширение это всего лишь вспомогательный инструмент косвенного применения. Иными словами, использовать его в качестве основного инструмента совершенно точно не получится. Кроме того, здесь есть одна дополнительная особенность. Расширение Фибоначчи очень часто пересекается по данным с волновой теорией (Элиотт). Дело все в том, что расширение нередко применяют для выявления точки завершения очередной волны цены.
Но этот инструмент еще и заметно отличается механикой своей работы. Постройка расширения начинается не с двух точек, а уже с трех. Все начинается по линии первичного импульса цены. Потом все достраивается по линии коррекции. Если тренд восходящий, то выбираем минимальное значение цены, в качестве точки опоры. Если же тренд нисходящий, то выбирайте максимальную цену. Тут все очень просто.
И вместе с тем, не стоит вдохновляться одним лишь инструментом. Постарайтесь не допустить того, чтобы закон золотого сечения не ввел вас в заблуждение. Конечно, прямой связи тут нет, но именно золотому сечению сегодня присваивают какие-то невероятные свойства. Точно так же трейдеры нередко запутываются, и начинают делать ставку исключительно на последовательность фибоначчи. А этого рынок не прощает, ведь это лишь один из инструментов. И он далеко не единственный, как вы понимаете.
Краткая история использования уровней и последовательностей в трейдинге
Математик, упомянутый нами в самом начале, представлял последовательность в виде задачи с кроликами. Позже станет понятно, что на одних кроликах весь свет не сошелся. Как оказалось, последовательность чисел, которую потом начнут ассоциировать с Фибоначчи, может быть применена в других сферах. Например, можно найти ее в космосе. Или в океане. А еще можно применять ее для торговли на фондовом рынке.
Как раз в трейдинге сумели заметить, что нередко, коррекция от текущего тренда начинает подозрительным образом вписываться в базу значений последовательности Фибоначчи. И отразить последовательность можно в виде процентов. А движение тренда будет равным интервалу от низшей точки (0 процентов). До высшей точки в 100 процентов. Естественно, для восходящих и нисходящих движений эти уровни будут различаться. И назвать это уровнями Фибоначчи не удастся, потому что диапазон 0-100 нужен просто для выставления границ, в которых и будет вылавливаться диапазон.
Как раз на базе этой особенности и были построены различные торговые индикаторы и инструменты. Мы уже разобрались с дугами и веером. Но помимо этого, есть временные зоны и другие инструменты, которые сегодня даже включаются в функционал самых популярных терминалов, в том числе и платформы Квик, о которой, наверное, слышал каждый профессиональный трейдер.
Торговать по уровням фибоначчи не так уж и просто, как может показаться в самом начале. Мы уже разобрались с тем, что этот инструментарий дает начинающему трейдеру:
- Определяется наличие тренда и признаков, указывающих на него.
- Определяется момент коррекции или завершение.
Все рассматривать сегодня не будем, пробежимся лишь по базовым моментам. Принято считать, что пробой уровня в 61.8 уже означает слом тренда. А если цена пробила уровень Фибо без отскока, то такой сигнал будет проигнорирован в 95% случаев. 5 процентов оставляем на исключительные ситуации, когда другие индикаторы и прогнозы вступили в прямое противоречие с данными по уровням Фибоначчи.
Если же коррекционное развитие уже началось, и оно случилось против нисходящего тренда с доминантой, то нужно следить за ценой. Если она пройдет до уровня фибо, а потом отскочит ниже, то открывается сделка на продажу. Это не прямая инструкция к действиям, а лишь ознакомительный пример для понимания.
Заключение
Ну и на этом пожалуй закончим. Сегодня мы разобрались с тем, что такое последовательность Фибоначчи. Узнали где ее применяют, рассказали вам о золотом сечении. И совершили экскурс в мир неожиданной и интересной математики, о которой редко рассказывают в школе.
Важно! По всем вопросам, если не знаете, что делать и куда обращаться:
Звоните 8-800-777-32-16.
Бесплатная горячая юридическая линия.